In this post we will see how time series decomposition work. This is not the original breakdown of the statsmodels seasonal decomposition instead this post will help to understand each and every component of the decomposition process.

Code Link :: GitHub Repository

Background

Here we will use the below simple equation to break down the time series.

\[TS = trend + seasonality + residual\]

We are assuming that the time sereis is built using only 3 components and i.e. trend, seasonality, residual.

In the following steps we will try to find each of the component of the time series.

Steps

Below is the plot for the original time series data.

Original Time Series data

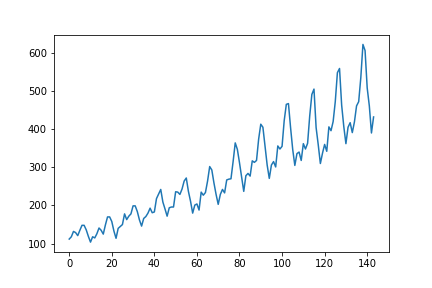
Step 1 :: Detrending Time series

Step 1.1 :: Find Approximate Trend

In the time series data fit a \(n\) degree polynomial. I went with \(n=2\) as most of the trend lines are less degree polynomial.

This will give us a trend line which is not the final one.

ApproximateTrend

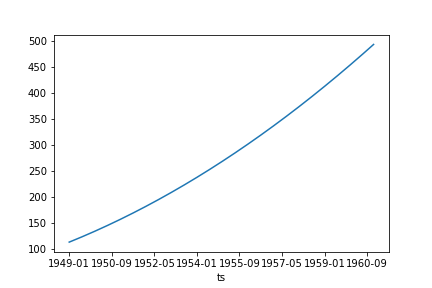
Step 1.2 :: Remove the approx. trend from the data

Here we will simple substact the data with the approx trend.

\[detrended = TS - approxTrend\]

Now we are left with a detrended data.

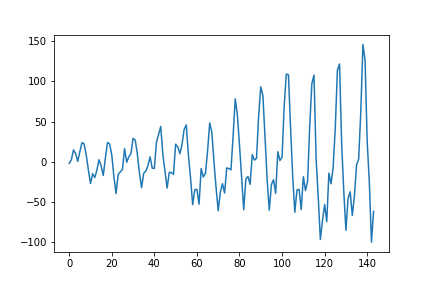
Approximate De-Trended Time Series

Step 2 :: Find Seasonality

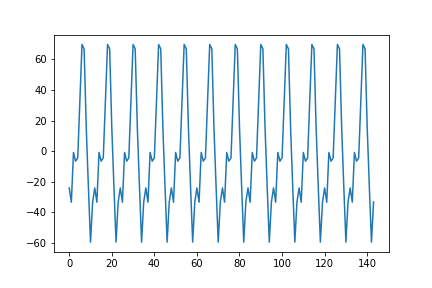
Step 2.1 :: Group data

Here we need to group the data as per required periods. I am going with 12 months seasonal period with this data. We will find average for all the months over all the years.

Step 2.2 :: Fill the monthly values

As we selected monthly periods we will have 12 records and 1 for each month. Now from the above step we fill the same monthly average value for all the years.

Seasonality

Step 3 :: Find Trend

Step 3.1 :: De-seasonalise data

Now to find deseasonal data we can simply subtract the seasonality from the original data

\[deseasoned = TS - seasonality\]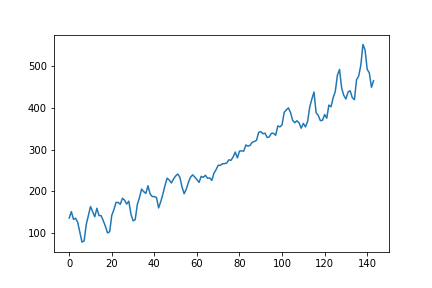

De-Seasoned Time Series

Step 3.2 :: Calculate Trend

In the ablove deseasoned data fit a \(n\) degree polynomial. I went with \(n=2\) as most of the trend lines are less degree polynomial.

This will give us the final trend line.

Trend

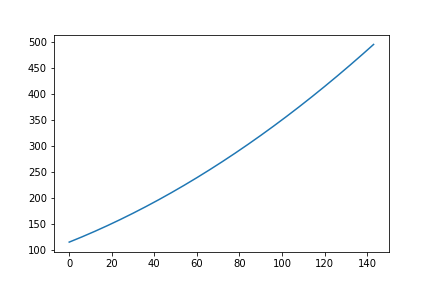
Step 4 :: Calculate Residual

We have all the components to calculate the residual now.

\[residual = TS - seasonality - trend\]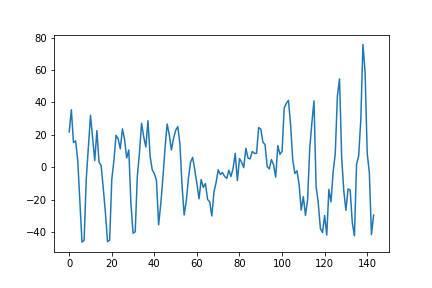

Residual

Conclusion

We have successfully broken down a time series into three components namely trend, seasonality and residual.

Trend

Seasonality

Residual

The results may not exactly match with the current way of decomposing a time series using statsmodels.