What is Cellex Rapid test?
Qualitative detection of IgM and IgG antibodies against SARS-CoV-2 in serum, plasma (EDTA or citrate), or venipuncture whole blood from individuals suspected of COVID-19 by their healthcare provider. Emergency use of this test is limited to authorized laboratories.
The Test
The test cassette consists of:
- a burgundy colored conjugate pad containing SARS-CoV-2 recombinant antigens (S and N proteins) conjugate with colloidal gold (SARS-CoV-2 conjugates) and rabbit IgG-gold conjugates;
- a nitrocellulose membrane strip containing an IgG line (G Line) coated with anti-human IgG, an IgM line (M Line) coated with anti-human IgM, and the control line (C Line) coated with goat anti-rabbit IgG.
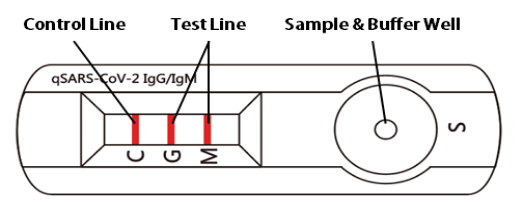
Assay
Valid Assay
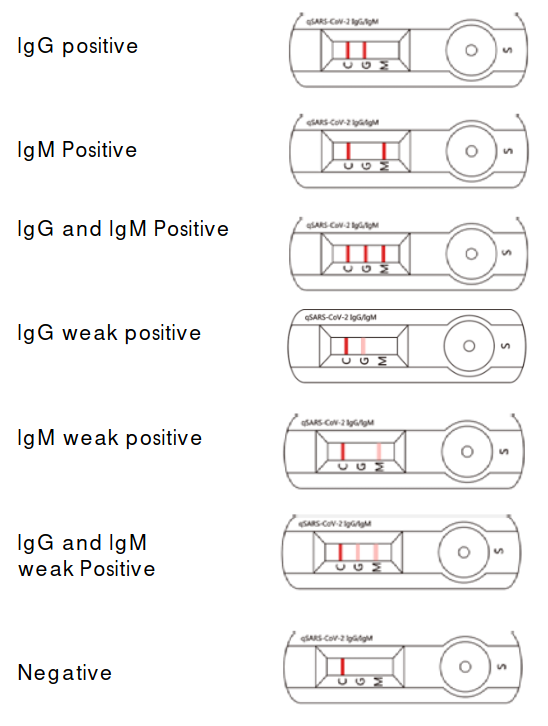
Invalid Assay
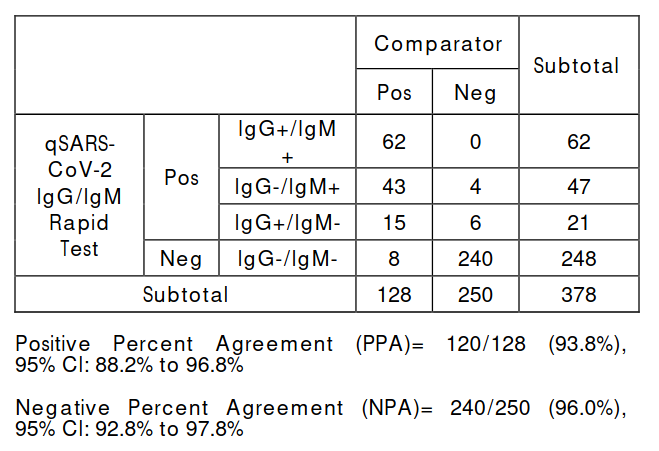
Accuracy Matrix
Given that the person has a positive test result, what is the probability that person has antibodies?
Here we will use Bayes Theorm to find out the probability.
Note: The result might be surprising for someone not from this field.
$ P( Test \vert Covid ) = 0.938$ is the probability for the true test given the person has COVID i.e. the Positive Percent Agreement(PPA).
$P(\neg Test \vert \neg Covid)$ is the probability of the negative test given there is no antibody in the blood stream.
If a random person is uniformly selected from a population and try this test out and is positive (I.e. three stripes lights up)
If we use the bayes theorm and
\[\begin{array}{l} P( \ Covid\ |\ Test\ ) \ =\ \frac{P( \ Test\ |\ Covid\ ) \ \bullet \ P( \ Covid\ )}{P( \ Test\ |\ Covid\ ) \ \bullet \ P( \ Covid\ ) \ +\ P( \ Test\ |\ \neg Covid)) \ \bullet \ P( \ \neg Covid\ )}\\ \\ \Longrightarrow \ \frac{P( \ T\ |\ C\ ) \ \bullet \ P( \ C\ )}{P( \ T\ |\ C\ ) \ \bullet \ P( \ C\ ) \ +\ (1-P( \ \neg T\ |\ \neg C\ )) \ \bullet \ ( 1-P( \ C\ ))}\\ \\ \Longrightarrow \ \frac{0.938\ \bullet \ P( \ C\ )}{0.938\ \bullet \ P( \ C\ ) \ +\ 0.04\ \bullet \ ( 1-P( \ C\ ))}\\ \\ \Longrightarrow \ \frac{0.938\ \bullet \ P( \ C\ )}{0.898\ \bullet \ P( \ C\ ) \ +\ 0.04} \end{array}\]Here, $P(C)$ is the probability of getting COVID.
Now, let us consider the value of $P(C) = 0.013$.
Then, the value of $P(C \vert T)= 0.2359$
So, the posterior probability to actually have the immunity given you get a positive test is just 23.59%.
Now, if we double or tripple the probability of $P(C)$ (the porobability of getting Covid) for the frontline workers then, If $P(C) = 0.026$ then the value of $P(C \vert T) = 0.3849$.
We will just plot $P(C)$ v/s $P(C \vert T)$ for values $P(C) \in range(0,0.2)$ that is a person whose chance of getting COVID is 20%(which is a very unlikey case).
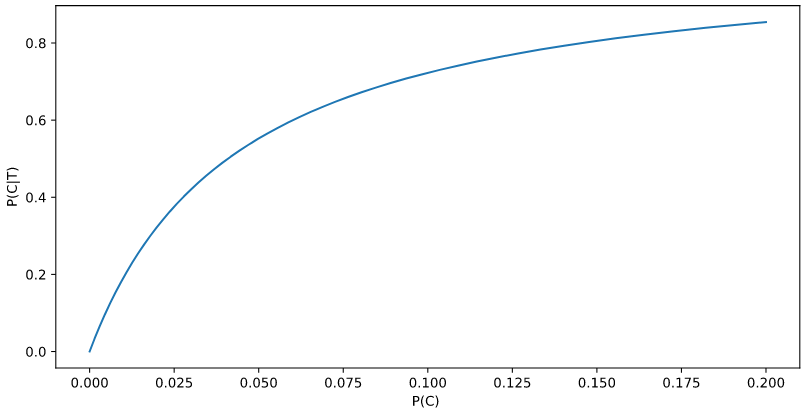
We can see the value of $P(C \vert T)$ converges to 1 when the value of $P(C) > 0.2$
